ALV树：自平衡二叉查找树/平衡二叉树/二叉平衡树

一、为什么要有平衡?叉树

?叉搜索树?定程度上可以提?搜索效率，但是当原序列有序时，例如序列 A = {1，2，3，4，

5，6}，构造?叉搜索树如图。依据此序列构造的?叉搜索树为右斜树，同时?叉树退化成单链表，搜索效率降低为 O(n)

?叉搜索树的查找效率取决于树的?度，因此保持树的?度最?，即可保证树的查找效率。同样

的序列 A，将其改为图示的?式存储，查找元素 6 时只需?较 3 次，查找效率提升?倍。

可以看出当节点数??定，保持树的左右两端保持平衡，树的查找效率最?。这种左右?树的?度相差不超过 1 的树为平衡?叉树。

二、定义

平衡因子：一个节点的平衡因子是其左右子树的高度差

对BST加上限制：每个节点的平衡因子的绝对值不超过1-------->AVL树

官方定义：

AVL树有如下性质：

1、可以是空树。

2、假如不是空树，任何?个节点的左?树与右?树都是平衡?叉树，并且?度之差的绝对值不超

过 1。

平衡之意，如天平，即两边的分量?约相同。

如下图

该树就不是平衡?叉树，因为结点60的左右子树高度差绝对值超过了1

该图就是?颗平衡?叉树。

三、AVL树如何进行插入操作

最?失衡?树：在新插?的节点向上查找，以第?个平衡因?的绝对值超过 1 的节点为根的?树

称为最?不平衡?树。也就是说，?棵失衡的树，是有可能有多棵?树同时失衡的。?这个时候，我们

只要调整最?的不平衡?树，就能够将不平衡的树调整为平衡的树。

插入过程中，如果插入某个节点后失衡，对该树进行调整，使其恢复平衡

调整的过程就是旋转（ALV树的重点）

旋转基本操作：当前x节点失衡，以x节点为中心进行旋转

下图为旋转大致原理：

1.左单旋

上图即为左单旋操作

代码实现思路：

设x是失衡节点，y=x->right //y是x调整前的右子树

(1) 把y的左子树变成x的右子树

x->right=y->left;

(2) x变成y的左孩子

y->left=x;

(3) return y

2.右单旋

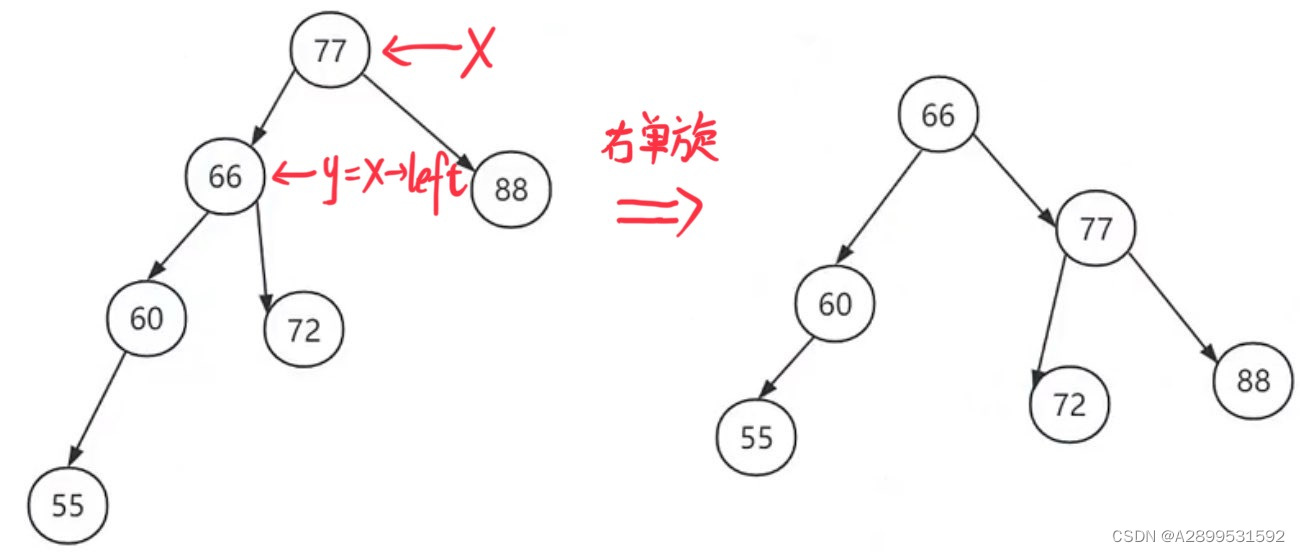
代码实现思路：

设x是失衡节点，y=x->left //y是x调整前的左孩子

(1) 把y的右孩子变成x的左孩子

x->left=y->right;

(2) x变成y的左孩子

y->right=x;

(3) return y

3.ALV树的查找，插入

1.查找：和BST一模一样

2.插入：插入一个数据x

（1）先按照BST的步骤进行插入

(2)算插入节点的所有祖先节点的平衡因子。----->高度差(get某个节点高度的函数）

节点x的高度x->h=max(x->left->h,x->right->h)+1;( h是高 )

节点的平衡因子：x的平衡因子为：x->left->h-x->right->h

（3）判断失衡：假设失衡节点x高度差为2

3.1）先看x->left和x->right谁高

3.2）再去高的子树里面去看根节点的哪边的子树高（去看x的孙节点的高度大小关系）

（4）调用对应的调整函数使树重新平衡

优先调整最小失衡子树

调整的类型有4种：假设最小失衡子树的根节点为A

LL：往A的左孩子的左子树中插入了一个节点，导致A的左子树比右子树高

调整策略：以A为中心右旋

LR：往A的左孩子的右子树中插入了一个节点，导致A的左子树比右子树高

（1）以A->left为中心进行左旋，转化为LL

（2）以A为中心右旋

RR：往A的右孩子的右子树中插入了一个节点，导致A的右子树比左子树高

以A为中心左旋

RL：往A的右孩子的左子树中插入了一个节点，导致A的右子树比左子树高

（1）以A->right为中心进行右旋，转化为RR

（2）以A为中心左旋

4.插入操作完整代码

#include <stdlib.h>
#include <stdio.h>
# include <string.h>
/*AVL树代码*/
//AVL树的节点结构
typedef struct AVLNode{
	int data;//数据域
	struct AVLNode* left; 
	struct AVLNode* right;
	int h;//该节点的高度
}AVLNode,*AVLtree; 

int max(int a,int b)
{
	return a>b?a:b;
 } 
//得到树的高，不能直接写x->h，因为x可能是NULL
int geth(AVLtree ro)
{
	if(ro==NULL)
	{
		return 0;
	}
	else{
		return ro->h;
	}
 } 

AVLtree initAVLtree(int k)
{
	AVLNode* root=(AVLNode*)malloc(sizeof(AVLNode));
	root->data=k;
	root->left=root->right=NULL;
	root->h=1;
	return root; 
}
//四种失衡的调整函数
//LL-->以失衡节点x为中心，右旋
AVLtree LL_rotation(AVLtree x)
{
	AVLNode* y=x->left;
	x->left=y->right;
	y->right=x;
	x->h=max(geth(x->left),geth(x->right))+1;
    y->h=max(geth(y->left),geth(y->right))+1;
	return y;
} 
//RR-->以失衡节点x为中心，左旋
AVLtree RR_rotation(AVLtree x)
{
	AVLNode* y=x->right;
	x->right=y->left;
	y->left=x;

	x->h=max(geth(x->left),geth(x->right))+1;
    y->h=max(geth(y->left),geth(y->right))+1;
    return y;
}
//LR--->以失衡节点x->left为中心，左旋.然后以失衡节点x为中心，右旋
AVLtree LR_rotation(AVLtree x)
{
	x->left=RR_rotation(x->left);
	x= LL_rotation(x);
	return x;
}
//RL--->以失衡节点x->right为中心，右旋.然后以失衡节点x为中心，左旋
AVLtree RL_rotation(AVLtree x)
{
	x->right=LL_rotation(x->right);
	x= RR_rotation(x);
	return x;
}
	
AVLtree insert_AVL(AVLtree root,int k)
{

	if(root==NULL)
	{
		AVLNode* s=(AVLNode*)malloc(sizeof(AVLNode));
		s->data=k;
		s->left=s->right=NULL;
		s->h=1;
		return s;
	}
	else if(k<root->data)
	{
		root->left=insert_AVL(root->left,k);
		//判断root是否失衡：LL LR 
		if(geth(root->left)-geth(root->right)>1) 
		{
			AVLNode* l=root->left;
			if(k < l->data )//或者   if(geth(l->left)>geth(l->right)) 
			{//LL
				root=LL_rotation(root);
			}
			else
			{//LR
				root=LR_rotation(root);
			}
		} 
		
	
	 } 
	 else if(k>root->data)
	 {
	 	root->right =insert_AVL(root->right ,k);
		//判断root是否失衡：RR  RL
		if(geth(root->right )-geth(root->left )>1) 
		{
			
			AVLNode* r=root->right ;
			if(k > r->data )
			{//RR
				root=RR_rotation(root);
			}
			else
			{//Rl
				root=RL_rotation(root);
			}
		} 
	 }
	  root->h=max(geth(root->left),geth(root->right))+1;
	 return root;
 } 
void inorder(AVLtree root)
{
	if(root!=NULL)
	{
		inorder(root->left );
		printf("%d %d
",root->data,root->h);
		inorder(root->right);
	}
}
int main()
{
	int n;
	int a[105];
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}
	AVLtree root=initAVLtree(a[1]);
	for(int i=2;i<=n;i++)
	{
		root=insert_AVL(root,a[i]);
	}
	inorder(root);
	
	return 0;	
}

四、AVL树的删除

假设在一棵AVL树中删除一个数据k

（1）执行BST的删除操作

BST删除：k在节点中

1.1）x度为0/1：直接删除节点，x唯一的孩子顶替x的位置

1.2）x度为2：找x的中序遍历前驱节点或后继节点y，x->data=y->data,问题转化成删除y节点

中序遍历前驱节点：x左子树中最靠右的节点（左子树中数据值最大）

中序遍历后继节点：x右子树中最靠左的节点（右子树中数据值最小）

（2）判断失衡：假设在x的子树中删除了一个节点，失衡节点是节点

当在x的左子树中删除一个节点时，左子树高度减一，导致失衡。看成：右子树一棵树也陪着左子树删了一个节点，但是又插入回来了，此时就变成插入导致的失衡了。

在x节点的一边的子树中删除了一个节点，就等价于在其另一边子树插入了一个节点导致的失衡--------->删除的失衡类型及调整方式和插入的失衡类型及调整方式一摸一样。

左删除相当于右边插入：RR 、RL

右删除相当于左边插入：LL 、LR

如下为例子：

可以看出删掉节点9以后该树能恢复平衡，因此该树等价于删掉节点9后再插入节点9，即LL型，以节点20为中心右旋即可恢复平衡。

特殊例子：

删掉节点30时，节点20的左孩子的左子树和右子树的节点都需要删掉才能使树平衡，这时LL和LR都行（推荐用LL，步骤比较少），可以自己试试看两种方法都能使该树平衡。

代码：

AVLNode* find(AVLNode* l)//查找l的左子树的最右节点
{
	while(l->right!=NULL)
	{
		l=l->right;
	}
	return l;
}
//在以root为根的树中删除k     
AVLtree AVL_de(AVLtree root,int k)
{
	if(root==NULL)
	{
		return NULL;
	}
	if(k<root->data)
	{
		root->left=AVL_de(root->left,k);
		//判断root失衡
		if( geth(root->right) - geth(root->left) >1)
		{//RR RL
			AVLNode* r=root->right;
			if( geth(r->right) >= geth(r->left) )
			{//RR	
				root=RR_rotation(root);
			}
			else
			{//RL
				
				root=RL_rotation(root);
			}
		} 
	}
	else if(k>root->data)
	{
		root->right =AVL_de(root->right ,k);
		//  LL LR
		if( geth(root->left) - geth(root->right) >1 )
		{//LL LR
			AVLNode* l=root->left;
			if( geth(l->left) >= geth(l->right) )
			{
				root=LL_rotation(root);
			}
			else{
				root=LR_rotation(root);
			}
		 } 
	}
	else
	{
		if(root->left!=NULL&&root->right!=NULL)
		{
			AVLNode* maxNode=find(root->left);
			root->data=maxNode->data;
			root->left=AVL_de(root->left,maxNode->data);                                                                   
			if( geth(root->right) - geth(root->left) >1)
			{//RR RL
				AVLNode* r=root->right;
				if( geth(r->right) >= geth(r->left) )
				{//RR	
					root=RR_rotation(root);
				}
				else
				{//RL
					root=RL_rotation(root);
				}
			} 
		}
		else
		{
			AVLNode* x=root;
			if(root->left!=NULL)
			{
				root=root->left;	
			}
			else
			{
				root=root->right;	
			}
			free(x);
			x=NULL;
			return root;	
		}
		
	}
	root->h=max(geth(root->left),geth(root->right))+1;
	return root;
}

五、AVL树插入和删除操作的完整代码

#include <stdlib.h>
#include <stdio.h>
# include <string.h>
/*AVL树代码*/
//AVL树的节点结构
typedef struct AVLNode{
	int data;数据域
	struct AVLNode* left; 
	struct AVLNode* right;
	int h;//该节点的高度
}AVLNode,*AVLtree; 

int max(int a,int b)
{
	return a>b?a:b;
 } 
//得到树的高，不能直接写x->h，因为x可能是NULL
int geth(AVLtree ro)
{
	if(ro==NULL)
	{
		return 0;
	}
	else{
		return ro->h;
	}
 } 

AVLtree initAVLtree(int k)
{
	AVLNode* root=(AVLNode*)malloc(sizeof(AVLNode));
	//
	root->data=k;
	root->left=root->right=NULL;
	root->h=1;
	return root; 
}
//四种失衡的调整函数
//LL-->以失衡节点x为中心，右旋
AVLtree LL_rotation(AVLtree x)
{
	AVLNode* y=x->left;
	x->left=y->right;
	y->right=x;
	x->h=max(geth(x->left),geth(x->right))+1;
    y->h=max(geth(y->left),geth(y->right))+1;
	return y;
} 
//RR-->以失衡节点x为中心，左旋
AVLtree RR_rotation(AVLtree x)
{
	AVLNode* y=x->right;
	x->right=y->left;
	y->left=x;

	x->h=max(geth(x->left),geth(x->right))+1;
    y->h=max(geth(y->left),geth(y->right))+1;
    return y;
}
//LR--->以失衡节点x->left为中心，左旋.然后以失衡节点x为中心，右旋
AVLtree LR_rotation(AVLtree x)
{
	x->left=RR_rotation(x->left);
	x= LL_rotation(x);
	return x;
}
//RL--->以失衡节点x->right为中心，右旋.然后以失衡节点x为中心，左旋
AVLtree RL_rotation(AVLtree x)
{
	x->right=LL_rotation(x->right);
	x= RR_rotation(x);
	return x;
}
	
AVLtree insert_AVL(AVLtree root,int k)
{

	if(root==NULL)
	{
		AVLNode* s=(AVLNode*)malloc(sizeof(AVLNode));
		s->data=k;
		s->left=s->right=NULL;
		s->h=1;
		return s;
	}
	else if(k<root->data)
	{
		root->left=insert_AVL(root->left,k);
		//判断root是否失衡：LL LR 
		if(geth(root->left)-geth(root->right)>1) 
		{
			AVLNode* l=root->left;
			if(geth(l->left)>geth(l->right))
			//或者  if(k < l->data )
			{//LL
				root=LL_rotation(root);
			}
			else
			{//LR
				root=LR_rotation(root);
			}
		} 
		
	
	 } 
	 else if(k>root->data)
	 {
	 	root->right =insert_AVL(root->right ,k);
		//判断root是否失衡：RR  RL
		if(geth(root->right )-geth(root->left )>1) 
		{
			
			AVLNode* r=root->right ;
			if(geth(r->right )>geth(r->left))
			//if(k > r->data )
			{//RR
				root=RR_rotation(root);
			}
			else
			{//Rl
				root=RL_rotation(root);
			}
		} 
	 }
	// root->h=max(root->left->h,root->right->h)+1;//bug 
	root->h=max(geth(root->left),geth(root->right))+1;
	 return root;
 } 
 //-----------------------------------------------------------------
AVLNode* find(AVLNode* l)//查找l的左子树的最右节点
{
	while(l->right!=NULL)
	{
		l=l->right;
	}
	return l;
}
//在以root为根的树中删除k     
AVLtree AVL_de(AVLtree root,int k)
{
	if(root==NULL)
	{
		return NULL;
	}
	if(k<root->data)
	{
		root->left=AVL_de(root->left,k);
		//判断root失衡
		if( geth(root->right) - geth(root->left) >1)
		{//RR RL
			AVLNode* r=root->right;
			if( geth(r->right) >= geth(r->left) )
			{//RR	
				root=RR_rotation(root);
			}
			else
			{//RL
				
				root=RL_rotation(root);
			}
		} 
	}
	else if(k>root->data)
	{
		root->right =AVL_de(root->right ,k);
		//  LL LR
		if( geth(root->left) - geth(root->right) >1 )
		{//LL LR
			AVLNode* l=root->left;
			if( geth(l->left) >= geth(l->right) )
			{
				root=LL_rotation(root);
			}
			else{
				root=LR_rotation(root);
			}
		 } 
	}
	else
	{
		if(root->left!=NULL&&root->right!=NULL)
		{
			AVLNode* maxNode=find(root->left);
			root->data=maxNode->data;
			root->left=AVL_de(root->left,maxNode->data);                                                                   
			if( geth(root->right) - geth(root->left) >1)
			{//RR RL
				AVLNode* r=root->right;
				if( geth(r->right) >= geth(r->left) )
				{//RR	
					root=RR_rotation(root);
				}
				else
				{//RL
					root=RL_rotation(root);
				}
			} 
		}
		else
		{
			AVLNode* x=root;
			if(root->left!=NULL)
			{
				root=root->left;	
			}
			else
			{
				root=root->right;	
			}
			free(x);
			x=NULL;
			return root;	
		}
		
	}
	root->h=max(geth(root->left),geth(root->right))+1;
	return root;
} 


//---------------------------------------------------------
void inorder(AVLtree root)
{
	if(root!=NULL)
	{
		inorder(root->left );
		printf("%d %d
",root->data,root->h);
		inorder(root->right);
	}
}
int main()
{
	int n;
	int a[105];
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}
	AVLtree root=initAVLtree(a[1]);
	for(int i=2;i<=n;i++)
	{
		root=insert_AVL(root,a[i]);
	}
	inorder(root);
	int k;
	scanf("%d",&k);
	root=AVL_de(root,k);
	inorder(root);
	
	return 0;	
}