这道题的思路是先构建二叉树，然后层序遍历二叉树。将问题拆解：1.如何构建二叉树。2.如何测层序遍历二叉树。

1.构建二叉树
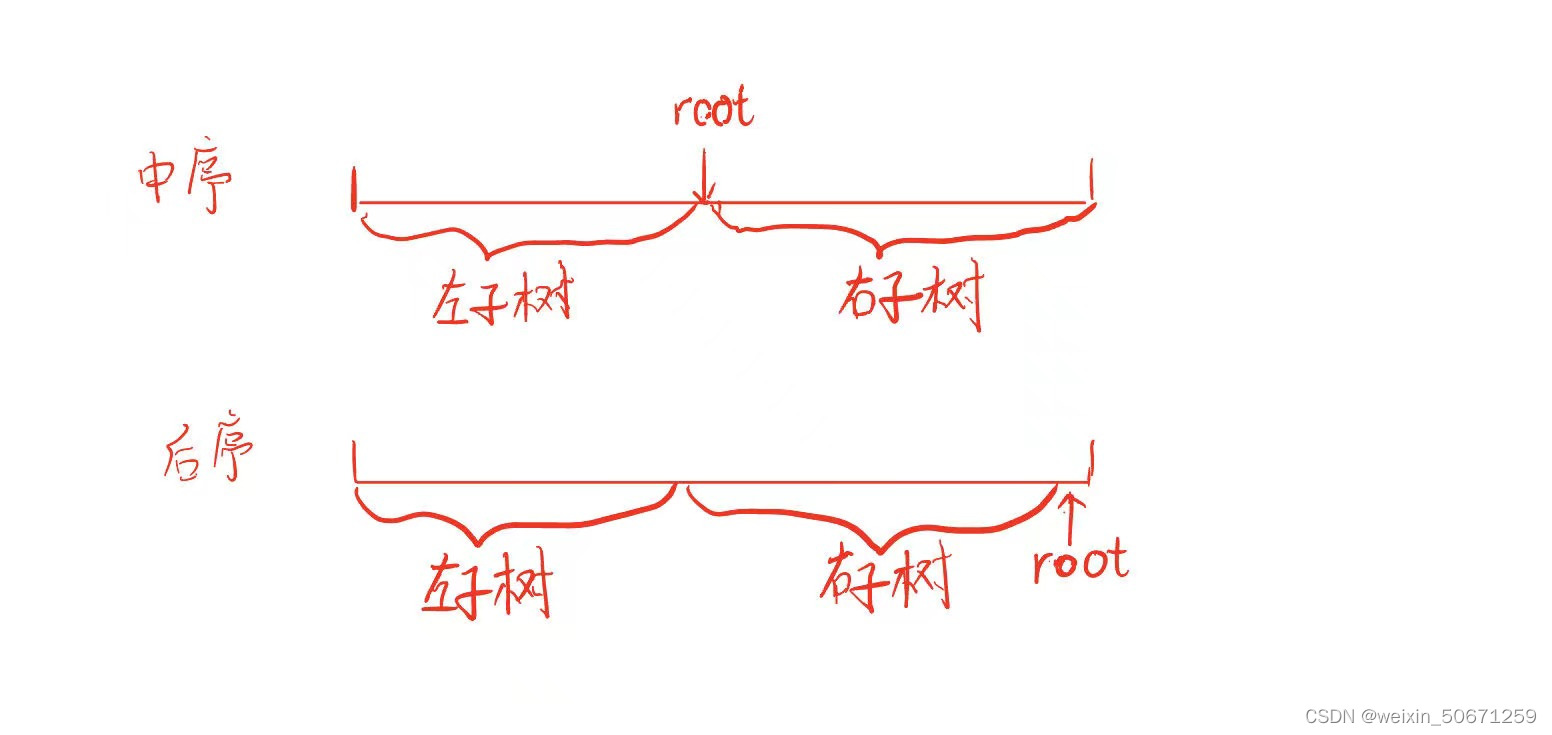
首先我们要知道一棵二叉树可由它的中序遍历和后序遍历确定：
（1）后序遍历的最后是该树或子树的根
（2）中序遍历根的左右分左子树和右子树

通过后序遍历找到根的值，然后再到中序序列里找到根的位置再将该树分为左子树与右子树 。不断递归即可通过中序和后序重塑一棵树。

int build(int il,int ir,int pl,int pr)//il，ir为中序遍历的左右下标；pl,pr为后序遍历的下标
{
    int root=postorder[pr]; //后序遍历的最后一位是树的根
    int k=pos[root];//pos数组记录了每个数的下标
    //根将中序遍历分成两部分，分别是左子树、右子树
    //l,r 为map，记录左右子树。
    if(il<k) l[root]=build(il,k-1,pl,k-1-il+pl);//k-1-il=x-pl  //左子树在中序序列中为[il,k-1] ，在后序序列中左子树长度相同，从pl开始，故 x-pl=k-1-il，x即右端点为k-1-il+pl；
    if(k<ir) r[root]=build(k+1,ir,pr-ir+k,pr-1);// pr-1-x=ir-k-1 //右子树在中序序列中为[k+1，ir] ，在后序序列中右子树长度相同，到pr-1结束，故 pr-1-x=ir-k-1，x即左端点为pr-ir+k；
    return root;
}

2.bfs层序遍历树

void bfs(int root)
{
    queue<int> q; 
    q.push(root);
    int flag=1;//标记是否第一次输出，第一次输出数组，后续输出空格数字；为了最后数字没有输出空格（pat格式要求）
    while(q.size()){
        int x=q.front();
        q.pop();
        if(flag){
            cout<<x;
            flag=0;
        }
        else cout<<" "<<x;
        if(l.count(x)) q.push(l[x]);//如果左节点在，则放入队列
        if(r.count(x)) q.push(r[x]);//如果有右节点，则放入队列
    }
}

整体代码：

#include<iostream>
#include<algorithm>
#include<string>
#include<unordered_map>
#include<queue>

using namespace std;
const int N=40;
int postorder[N],inorder[N];
unordered_map<int,int> l,r,pos;
int build(int il,int ir,int pl,int pr)
{
    int root=postorder[pr];
    int k=pos[root];
    if(il<k) l[root]=build(il,k-1,pl,k-1-il+pl);//k-1-il=x-pl
    if(k<ir) r[root]=build(k+1,ir,pr-ir+k,pr-1);// pr-1-x=ir-k-1
    return root;
}
void bfs(int root)
{
    queue<int> q;
    q.push(root);
    int flag=1;
    while(q.size()){
        int x=q.front();
        q.pop();
        if(flag){
            cout<<x;
            flag=0;
        }
        else cout<<" "<<x;
        if(l.count(x)) q.push(l[x]);
        if(r.count(x)) q.push(r[x]);
    }
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin>>postorder[i];
    for(int i=0;i<n;i++){
        cin>>inorder[i];
        pos[inorder[i]]=i;//pos存放每个数的下标
    }
    int root=build(0,n-1,0,n-1);//构建二叉树
    bfs(root);//层序遍历
    return 0;
}